Free Angle of Depression Calculator Online
When standing on an elevated point and looking downward at an object below, the invisible angle formed between your horizontal line of sight and the downward view is called the angle of depression. Whether you’re solving trigonometry problems, navigating, surveying land, or managing construction sightlines, understanding this angle is crucial. The Angle of Depression Calculator makes it easy to compute this angle with just two known values.
In this blog, we explore the concept of angle of depression, its real-world applications, the math behind it, how to use the calculator, and why it’s a critical tool in fields like engineering, navigation, architecture, and education.
Angle of Depression Calculator
What Is the Angle of Depression?
The angle of depression is the angle formed between a horizontal line of sight and a downward line toward an object. It’s measured from the horizontal downward and is always outside the triangle in practical setups but corresponds to the interior triangle angle using alternate interior angles.
Simple Definition:
The angle between the horizontal eye level of an observer and the line of sight to a lower object.
This is a key principle in right-angled triangle trigonometry.
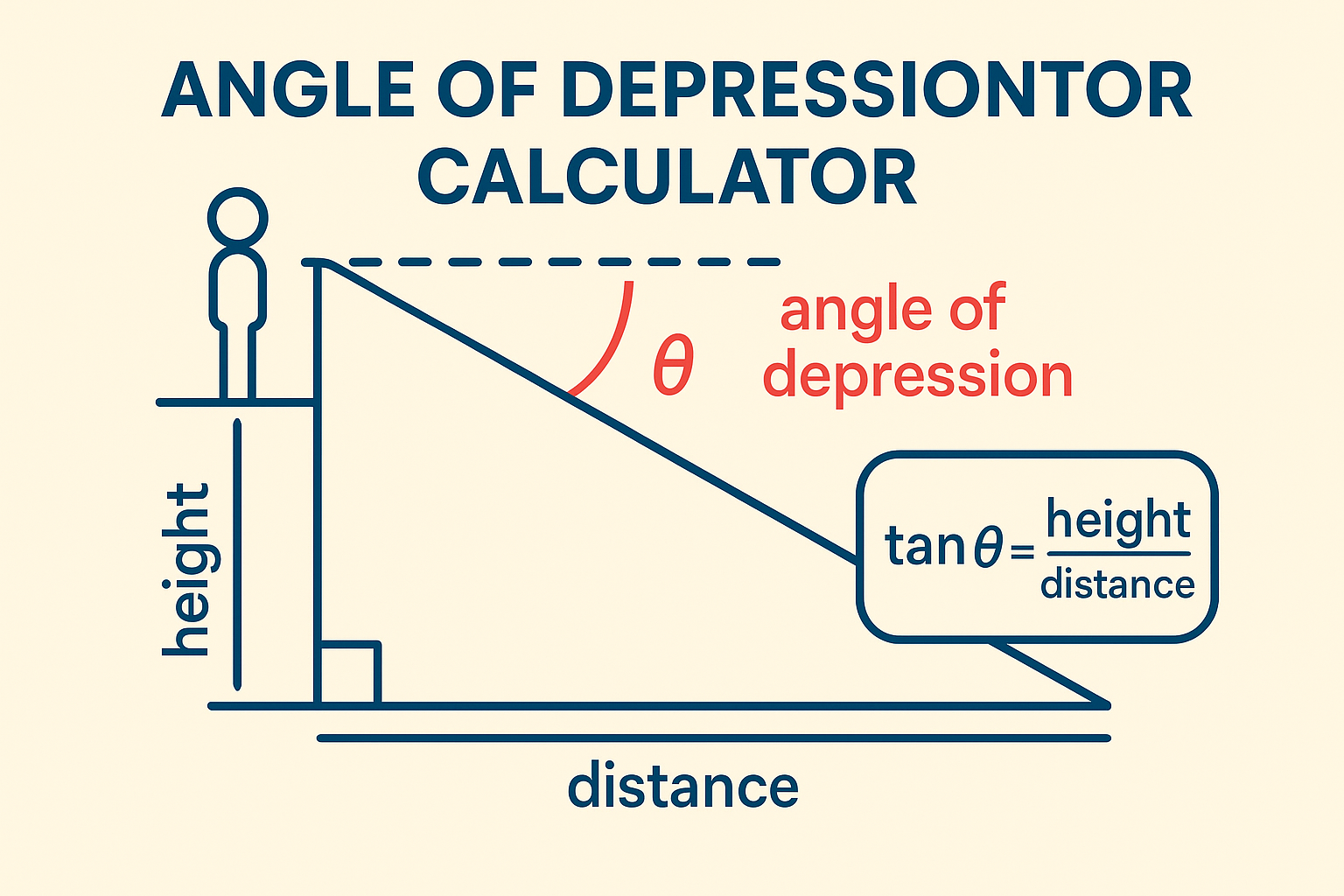
Visual Representation
To understand the angle of depression, imagine:
- You’re on a lighthouse platform, 60 feet above sea level.
- A boat is in the water, 300 feet away from the base of the lighthouse.
- The angle formed by your horizontal line of sight and the line from your eyes to the boat is the angle of depression.
This situation forms a right triangle, where:
- The horizontal distance is the adjacent side.
- The height difference (elevation) is the opposite side.
- The line of sight to the object is the hypotenuse.
Formula: Angle of Depression
The tangent function in trigonometry is commonly used: $$tan(θ)=Vertical DistanceHorizontal Distance\tan(\theta) = \frac{\text{Vertical Distance}}{\text{Horizontal Distance}}tan(θ)=Horizontal DistanceVertical Distance$$
To solve for the angle: $$θ=tan−1(Vertical DropHorizontal Distance)\theta = \tan^{-1} \left( \frac{\text{Vertical Drop}}{\text{Horizontal Distance}} \right)θ=tan−1(Horizontal DistanceVertical Drop)$$
Where:
- θ\thetaθ = Angle of depression (in degrees)
- Vertical drop = Elevation difference
- Horizontal distance = Base distance
Example Calculation
Problem:
You’re standing on a cliff 100 feet high. A boat is 500 feet from the base of the cliff. What is the angle of depression?
Solution: $$tan(θ)=100500=0.2\tan(\theta) = \frac{100}{500} = 0.2tan(θ)=500100=0.2 θ=tan−1(0.2)≈11.31∘\theta = \tan^{-1}(0.2) ≈ 11.31^\circθ=tan−1(0.2)≈11.31∘$$
Answer:
The angle of depression is approximately 11.31 degrees.
What Does an Angle of Depression Calculator Do?
An Angle of Depression Calculator is an online or digital tool that computes:
- The angle of depression
- The horizontal distance
- The vertical elevation difference
All you need is two known values, and the calculator solves the third. It’s based on right-triangle geometry and inverse tangent functions.
Input Fields in the Calculator
Most calculators include:
- Vertical height (elevation drop from the observer)
- Horizontal distance (distance from the observer to the object base)
- Angle (if known)
Depending on what you input, it will compute:
- Missing angle
- Missing height
- Missing distance
Use Cases of the Angle of Depression Calculator
1. Surveying & Topography
Surveyors use this concept to map elevation profiles, estimate slope declines, and measure ground angles.
2. Construction & Engineering
Used in planning:
- Drainage systems
- Ramps
- Roofing
- Slope stabilization
- Excavation angles
3. Aviation and Navigation
Pilots use angles of depression when descending toward a runway, ensuring proper landing alignment.
4. Physics & Ballistics
In projectile motion, the angle of depression affects trajectory, range, and impact point especially on elevated platforms.
5. Trigonometry & Education
Students use this to solve geometry problems involving right triangles, especially in:
- SATs
- GREs
- High school math classes
Related Trigonometric Functions
| Function | Formula | Use Case |
|---|---|---|
| Tangent | $$tan(θ)=OppositeAdjacent\tan(\theta) = \frac{\text{Opposite}}{\text{Adjacent}}tan(θ)=AdjacentOpposite$$ | Most common in angle of depression problems |
| Sine | $$sin(θ)=OppositeHypotenuse\sin(\theta) = \frac{\text{Opposite}}{\text{Hypotenuse}}sin(θ)=HypotenuseOpposite$$ | Used if hypotenuse is known |
| Cosine | $$cos(θ)=AdjacentHypotenuse\cos(\theta) = \frac{\text{Adjacent}}{\text{Hypotenuse}}cos(θ)=HypotenuseAdjacent$$ | For solving distances with known angles |
Note:
In depression problems, the adjacent is often the horizontal distance, and the opposite is the vertical drop.
Practical Example (Engineering)
Problem:
An engineer is placing a security camera on a pole 25 ft high. They want the camera to face a point 50 ft away on the ground. What is the angle of depression?
Solution: $$tan(θ)=2550=0.5\tan(\theta) = \frac{25}{50} = 0.5tan(θ)=5025=0.5 θ=tan−1(0.5)≈26.57∘\theta = \tan^{-1}(0.5) ≈ 26.57^\circθ=tan−1(0.5)≈26.57∘$$
Answer: 26.57 degrees.
This angle ensures the camera points directly at the target.
Angle of Depression vs Angle of Elevation
| Feature | Angle of Depression | Angle of Elevation |
|---|---|---|
| Direction of sight | Looking down | Looking up |
| Line of sight | Down from horizontal | Up from horizontal |
| Common Use | Surveying, flying, shooting | Viewing mountains, airplanes |
| Mathematically related? | Yes both measured from horizontal | Yes – alternate interior angles |
Fun fact:
They are numerically equal in ideal right-triangle geometry due to alternate interior angle properties.
Tools Used to Measure Angle of Depression
- Clinometer
- Protractor & Sightline
- Digital inclinometer
- Surveying level
- Angle of Depression Calculator
- GPS elevation + distance tools
Unit Consistency
Always ensure that both elevation and horizontal distance are in the same unit (feet, meters, inches, etc.). Otherwise, your result will be inaccurate.
| Convert from | To | Multiply by |
|---|---|---|
| Feet to Meters | M | 0.3048 |
| Meters to Feet | Ft | 3.28084 |
Common Mistakes to Avoid
- Confusing the angle with the slope
- Using different units for height and distance
- Forgetting to use inverse tangent when solving for angle
- Misidentifying triangle sides (opposite vs adjacent)
- Using vertical distance as hypotenuse
Advanced Features of Modern Calculators
Many online calculators offer:
- 3D visualizations
- Graphs of the sightline
- Auto unit conversion
- Mobile responsiveness
- Exportable result tables
- Step-by-step math breakdown
Some tools also double as:
- Slope angle calculators
- Elevation change calculators
- Projectile drop estimators
Classroom Application: Word Problem Example
Problem:
A student is standing on a 15-meter tower and sees a soccer ball on the ground. The ball is 45 meters away from the base of the tower. What is the angle of depression?
Solution: tan(θ)=1545=0.333\tan(\theta) = \frac{15}{45} = 0.333tan(θ)=4515=0.333 θ=tan−1(0.333)≈18.43∘\theta = \tan^{-1}(0.333) ≈ 18.43^\circθ=tan−1(0.333)≈18.43∘
Answer: 18.43 degrees
Teachers can use such examples to reinforce trigonometric understanding.
Summary Table
| Element | Details |
|---|---|
| Main Formula | θ=tan−1(Vertical DropHorizontal Distance)\theta = \tan^{-1} \left( \frac{\text{Vertical Drop}}{\text{Horizontal Distance}} \right)θ=tan−1(Horizontal DistanceVertical Drop) |
| Used In | Surveying, trigonometry, construction, physics |
| Inputs Needed | Vertical drop and horizontal distance |
| Output | Angle in degrees |
| Related Concept | Alternate interior angle (equal to angle of elevation from the other side) |
| Measurement Units | Consistent units (meters, feet, etc.) |
Conclusion
The Angle of Depression Calculator is a versatile, powerful tool designed to solve real-world and academic problems with ease. From solving math homework to planning construction sightlines, it delivers accuracy, efficiency, and confidence.
By understanding the relationship between elevation, distance, and viewing angles, you can apply the calculator to:
- Navigate safely
- Build correctly
- Survey accurately
- Teach effectively
Plug in the numbers, choose your units, and the angle of depression is instantly calculated no guessing, no struggle, just solid trigonometry at work.