Free Dome Volume Calculator Online

Domes are remarkable structures used in architecture, construction, landscaping, and engineering. From ancient cathedrals to modern sports arenas and backyard greenhouses, dome-shaped structures are praised for their strength, aesthetics, and efficient use of materials. But estimating the volume of a dome can be tricky without the right tools. That’s where the dome volume calculator comes in a fast and reliable method to determine the internal volume of any dome using a simple set of inputs.

This guide explains how dome volume calculations work, provides key formulas, and shows how to use a dome volume calculator effectively for various real-world projects.

Dome Volume Calculator

What Is a Dome?

A dome is a three-dimensional structure that resembles the upper half of a sphere. Domes can be fully hemispherical, segmental (less than a hemisphere), or even elliptical depending on design requirements. Common uses include planetariums, greenhouses, silos, observatories, and religious structures.

The primary goal when calculating dome volume is to estimate the internal capacity how much air, material, or liquid it can hold. This is especially useful in architecture, plumbing, and construction planning where volume directly affects material usage and cost.

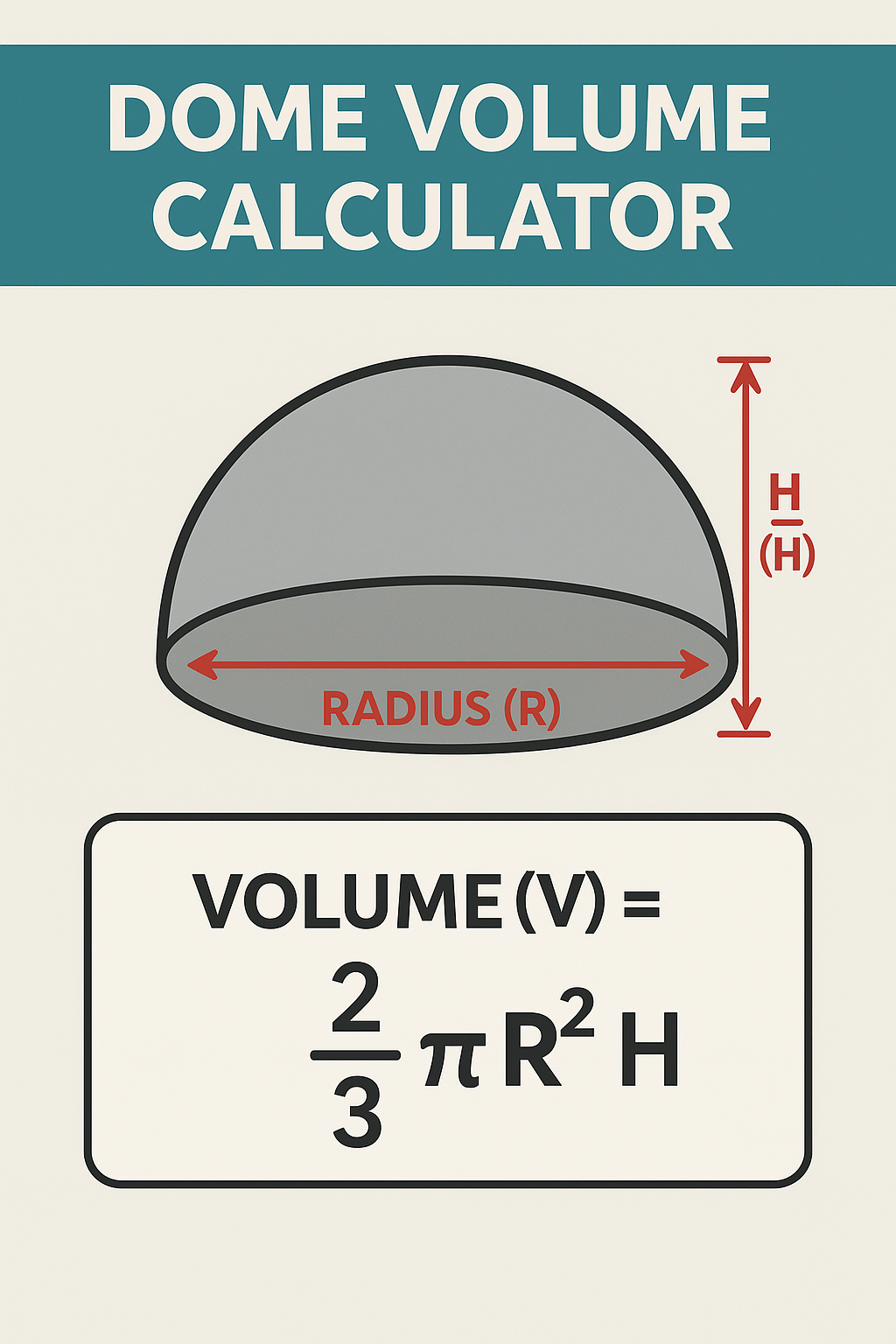
dome volume calculator

What Is a Dome Volume Calculator?

A dome volume calculator is a specialized digital tool or formula that calculates the internal volume of a dome structure based on two basic inputs:

  • Radius (or diameter)
  • Height of the dome

Using mathematical models, it computes the volume in cubic units, typically cubic feet, meters, or inches, depending on your settings.

Why Is Dome Volume Important?

Knowing the dome volume is essential for multiple reasons:

  • Calculating storage or interior capacity
  • Determining HVAC or ventilation needs
  • Estimating materials for insulation or finishing
  • Planning liquid containment in tanks or domed pools
  • Ensuring efficient space utilization in architectural design

Whether you’re working on a concrete shell, wooden frame, or geodesic dome, accurate volume estimation leads to smarter planning and cost-effective execution.

Types of Domes Commonly Calculated

  • Hemispherical Dome – A perfect half-sphere; most common in classical design
  • Segmental Dome – A dome with height less than the radius
  • Elliptical or Parabolic Dome – Designed for aesthetics or specific structural performance
  • Geodesic Dome – Uses triangular elements; volume calculations still based on dome principles

Each type uses a variation of the same fundamental volume formulas, adapted slightly for height or curvature.

Dome Volume Formula

The most commonly used dome volume formula is for a spherical cap, which represents the upper part of a sphere (a dome). Here’s the formula: V=16πh(3a2+h2)V = \frac{1}{6} \pi h (3a^2 + h^2)V=61​πh(3a2+h2)

Where:

  • VVV = Volume of the dome
  • hhh = Height of the dome
  • aaa = Radius of the base

This formula works for any dome as long as you know the base radius and vertical height. If the dome is a perfect hemisphere, use the simplified formula: $$V=23πr3V = \frac{2}{3} \pi r^3V=32​πr3$$

Where:

  • rrr = Radius of the dome

These equations give you the internal volume, which can then be converted to gallons, liters, or any other desired unit.

Example: Calculating Dome Volume

Let’s say you’re building a hemispherical greenhouse with a radius of 6 meters. What is the internal volume? $$V=23πr3=23π(6)3=23π×216≈452.39 m3V = \frac{2}{3} \pi r^3 = \frac{2}{3} \pi (6)^3 = \frac{2}{3} \pi \times 216 \approx 452.39 \text{ m}^3V=32​πr3=32​π(6)3=32​π×216≈452.39 m3$$

This means the dome has a volume of approximately 452 cubic meters.

For a segmental dome with a base radius of 5 meters and height of 2 meters: $$V=16πh(3a2+h2)=16π×2(3×25+4)=16π×2×79≈82.67 m3V = \frac{1}{6} \pi h (3a^2 + h^2) = \frac{1}{6} \pi \times 2 (3 \times 25 + 4) = \frac{1}{6} \pi \times 2 \times 79 \approx 82.67 \text{ m}^3V=61​πh(3a2+h2)=61​π×2(3×25+4)=61​π×2×79≈82.67 m3$$

Inputs Required in a Dome Volume Calculator

Most dome volume calculators ask for:

  • Base Radius or Diameter – Core measurement from the center to the dome’s base edge
  • Height – Vertical distance from the base to the dome’s top
  • Unit of Measurement – Feet, meters, inches, etc.
  • Optional: Wall thickness or material density (for load or thermal calculations)

These inputs allow the tool to provide accurate outputs tailored to your project scale and unit preference.

Applications of Dome Volume in Construction

Dome volume isn’t just a math exercise. It influences real-world decisions across various industries:

  • Architecture – Volume determines insulation needs, airflow calculations, and space utilization
  • Engineering – Structural load calculations rely on enclosed volume
  • Agriculture – Used to size grain silos or compost domes
  • HVAC Design – Helps calculate air volume for heating or cooling systems
  • Event Venues – Determines how many people can be safely housed inside

Converting Dome Volume to Other Units

Once you have the dome volume in cubic meters, you may need to convert it:

  • Liters:

$$Volume (L)=Volume (m3)×1000\text{Volume (L)} = \text{Volume (m}^3) \times 1000Volume (L)=Volume (m3)×1000$$

  • Gallons (US):

$$Volume (gal)=Volume (m3)×264.172\text{Volume (gal)} = \text{Volume (m}^3) \times 264.172Volume (gal)=Volume (m3)×264.172$$

  • Cubic Feet:

$$Volume (ft3)=Volume (m3)×35.3147\text{Volume (ft}^3) = \text{Volume (m}^3) \times 35.3147Volume (ft3)=Volume (m3)×35.3147$$

This flexibility makes the dome volume calculator useful in both metric and imperial measurement systems.

When to Use a Dome Volume Calculator

Use the calculator during:

  • Concept design for domed structures
  • Planning greenhouse capacity
  • Sizing dome-covered storage tanks
  • Estimating materials like insulation or spray foam
  • Water volume management in dome-shaped ponds or reservoirs

Architects, landscapers, civil engineers, and even DIY builders all benefit from accurate dome volume estimates.

Tips for Accurate Dome Volume Calculation

  • Always measure from the base center to the outer radius—not inner
  • Include insulation layers or shell thickness only if needed for material estimates
  • Confirm if your dome is hemispherical or partial
  • Use the right formula version based on height vs. radius
  • Convert your units properly to avoid incorrect ordering or construction errors

Advantages of Using an Online Dome Volume Calculator

Manual calculations can be time-consuming and error-prone. A dome volume calculator gives you:

  • Fast results in real-time
  • Customizable input formats
  • Clean interface with instant conversions
  • Accuracy based on proven geometry formulas
  • Helpful for planning, purchasing, and presentations

Many JavaScript-based tools now offer dynamic form controls, making it easy to visualize the input-output relationship without installing software.

Limitations and Considerations

While calculators are accurate, they assume ideal geometry. Real-world construction imperfections like uneven bases, material bulges, or attached structures may slightly affect true volume. For precision in large-scale builds, follow up with professional CAD-based volume simulations.

FAQs

Q: Can I use the dome volume calculator for a geodesic dome?
Yes, as long as you calculate the height and radius properly. The shape is more complex, but the base volume follows the same rules.

Q: How do I find the radius if I only have the diameter?
Divide the diameter by 2.

Q: Will the calculator include shell thickness?
Some tools offer that option, but most focus on internal volume. For wall thickness, subtract it from the outer radius.

Q: Can I convert dome volume to weight?
Yes, by multiplying the volume by material density: $$Weight=Volume×Density\text{Weight} = \text{Volume} \times \text{Density}Weight=Volume×Density$$

Q: Is the dome volume the same as the area?
No. Volume is three-dimensional. Surface area of a dome is different and uses another formula.

Conclusion

Whether you’re building a backyard greenhouse, a luxury spa dome, or a commercial storage facility, the dome volume calculator is your go-to tool for fast, reliable volume estimates. By using just the radius and height, you can determine internal space, material needs, and airflow calculations with precision.

Understanding the geometry behind dome structures empowers smarter planning, better cost control, and smoother construction execution. Don’t rely on guesses or rough estimates. Use the calculator, apply the formulas, and build with confidence one accurate volume at a time.