Free Vertical Curve Calculator Online
In the world of transportation engineering, a precise and reliable vertical curve calculator is a critical tool used by civil engineers, designers, and planners to ensure smooth transitions between different grades in road design and railway construction. Whether you are designing highways, planning new rail lines, or evaluating existing infrastructure, the ability to quickly perform vertical curve calculations ensures safety, accuracy, and efficiency across all types of engineering projects.
Vertical Curve Elevation Calculator
What is a Vertical Curve?
A vertical curve is a curved segment in the vertical plane of a roadway or railway that provides a smooth transition between two grades. These curves are vital for road safety, rider comfort, and efficient vehicle performance on slopes. Common types of vertical curves include:
- Sag curves – where a road dips and then rises
- Crest curves – where a road rises and then dips
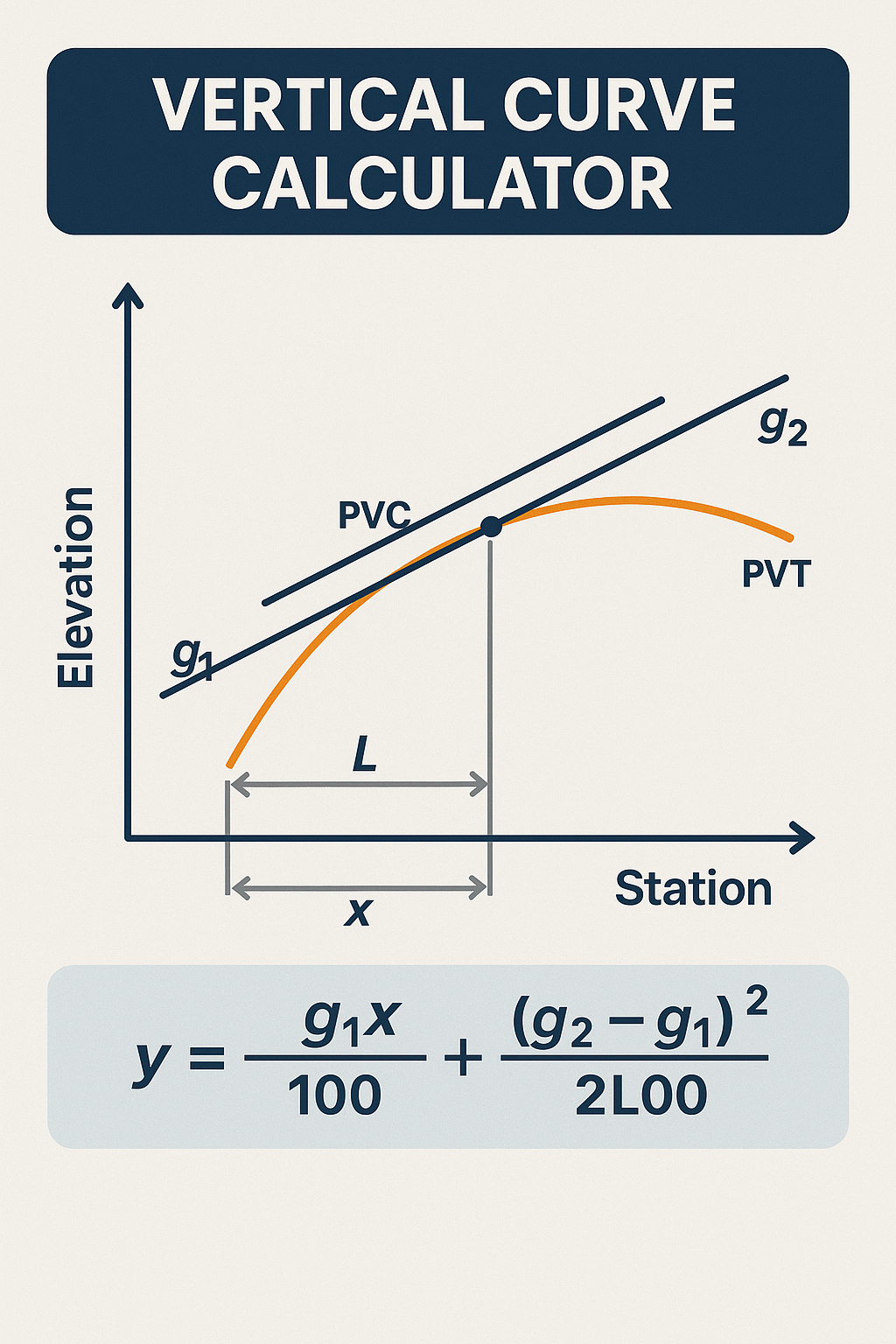
The geometry of these curves is defined by a mathematical equation typically a second-degree parabola, such as $$ax^2 + bx + c$$ that models the vertical alignment of the roadway. These calculations are important in determining the point of vertical curvature (PVC), point of vertical tangency (PVT), curve length, and offset distances.
Why Use a Vertical Curve Calculator?
Manual computation of vertical curvature can be complex and time-consuming, especially when considering large-scale transportation design projects. A vertical curve calculator simplifies this process by automating the mathematical equations needed for:
- Determining curve length
- Calculating elevation points
- Identifying PVC and PVT
- Finding the high or low point of the curve
- Estimating grades, distances, and offsets
It is an indispensable asset for any project involving roadways, rail tracks, or urban planning.
Key Components of Vertical Curves
To effectively use a vertical curve calculator, one must understand the parameters and engineering concepts behind vertical curve geometry:
1. PVC (Point of Vertical Curvature)
The starting point of the vertical curve, where the curve begins transitioning from the initial grade.
2. PVT (Point of Vertical Tangency)
The ending point of the curve where the roadway resumes a constant grade.
3. Length of the Curve (L)
Total horizontal distance between PVC and PVT.
4. Grades (G1 and G2)
These represent the initial and final grades before and after the curve.
5. Elevation Point
The elevation at a given point along the curve. Calculated using vertical curve equations.
6. Offset Distance
The vertical difference between the curve and the tangent line at a specific point.
Vertical Curve Calculator Formula
To calculate the elevation YYY at a given distance xxx from PVC: Y = $$Y_{PVC} + G_1 \cdot x + \frac{(G_2 – G_1)}{2L} \cdot x^2$$
Where:
- YYY = Elevation at distance xxx
- YPVCY_{PVC}YPVC = Elevation at PVC
- G1G_1G1 = Initial grade (%)
- G2G_2G2 = Final grade (%)
- LLL = Length of the curve
- xxx = Distance from PVC
This engineering formula ensures precise calculations for any vertical curve setup, whether it’s for road design, rail infrastructure, or highway projects.
Applications in Transportation Engineering
Vertical curve geometry plays a pivotal role in:
- Highways Engineering: Ensuring a smooth transition at slope intersections to maintain speed limits and road safety
- Railway Construction: Creating stable and comfortable paths for train travel
- Urban Planning: Designing ramps, overpasses, and grade-separated intersections
- Infrastructure Projects: Managing elevation changes in drainage systems and access roads
In each case, using a vertical curve calculator leads to accurate results, optimal geometry, and better project planning.
Examples of Vertical Curve Use
Example 1: Crest Curve on a Highway
An engineer is tasked with designing a crest vertical curve to connect a +3% upgrade to a -2% downgrade over a 500 ft curve length. Using the vertical curve calculator, they can determine:
- PVC and PVT locations
- Elevation points at various stations
- Highest point of the curve
- Offset distances to check clearance for overhead signs
Example 2: Railway Track Sag Curve
A rail design engineer planning a transition between two track grades (-1.5% to +1.0%) over 800 ft can use the tool to:
- Model the curve geometry
- Ensure safe acceleration and deceleration
- Align with safety regulations for curve radius and slope
Benefits of Using a Vertical Curve Calculator
Improves Roadway Safety
Allows engineers to meet design criteria for motorist visibility, vehicle dynamics, and safe braking distances.
Reduces Human Error
By automating complex calculations, the calculator ensures more accurate results than manual methods.
Saves Time
Accelerates the design process for large-scale roadway and railway projects.
Optimizes Resources
Efficient designs lead to better use of materials, minimizing construction costs and environmental impact.
Engineering and Infrastructure Integration
Modern engineering tools often integrate vertical curve calculators into broader systems:
- Excel tools for civil engineering workflows
- AutoCAD plugins for road alignment
- Online calculator tools used in transportation engineering
These tools contribute to improved efficiency, better geometry control, and more reliable infrastructure planning.
Using a Vertical Curve Calculator Online
An online vertical curve calculator offers:
- Input fields for grades, lengths, and starting elevations
- Automatic computation of curve geometry
- Graphical representation of vertical alignment
- Compatibility with road design standards
These calculators are essential for engineers, urban planners, and infrastructure designers who need a simple input system for complex calculations.
Common Terms Related to Vertical Curves
| Term | Description |
|---|---|
| BVC | Beginning of vertical curve |
| PVT | Point of vertical tangency |
| Sag Curve | Curve that dips before rising |
| Crest Curve | Curve that rises before dipping |
| Offset Distance | Difference between curve and tangent at a point |
| Vertical Tangency | Where a curve transitions into a straight grade |
| Grade (%) | The incline or decline of the road, expressed as a percent |
| High Point / Low Point | Maximum or minimum elevation on a vertical curve |
| PVC to PVT Length | Horizontal distance of the curve |
Real-World Infrastructure Projects
Many infrastructure projects rely heavily on vertical curve geometry:
- High-speed rail systems: Ensuring smooth transitions to maintain safety at high speeds
- Mountain roads: Managing sharp elevation changes with optimized curve lengths
- Urban flyovers: Designing compact vertical curves that fit tight roadway profiles
These projects show how important curve length, grade changes, and vertical curvature are to modern engineering.
Integration with Other Calculators
A vertical curve calculator often works alongside:
- Horizontal curve calculators
- Slope/grade calculators
- Sec inverse calculator for trigonometric functions
- Distance calculator for route planning
Together, these tools provide a complete design framework for transportation projects and civil engineering.
Final Thoughts
A vertical curve calculator is more than just a math tool it’s a strategic asset for professionals involved in construction, transportation design, and engineering projects. By ensuring precise calculations, safe transitions, and efficient alignments, this tool helps streamline infrastructure planning from urban roads to railway systems.
Whether you’re working with a curve design in Excel, or using an online calculator for a roadway project, understanding the importance of vertical curves is essential to producing safe, functional, and cost-effective designs.